Interactions¶
The ER has its own approach for adding interactions to the particle transport process. This approach is based on the ability of users to write their own Stepping Action for transport and the ability to add new tracks with defined properties to the track stack.
It allows to take into account energy losses of projectiles in the beam diagnostics system and the target. This is a necessity in low energy physics simulations.
Interaction position¶
We assume the exponential distribution of the interaction position along the trajectory of an ion inside the target. It could be true in the case of constant (energy independent) total interaction cross section. In reality we deal with a kind of approximation.
The survival probability \(p_s\) of an ion after passing the path \(x\) is:
where \(\Lambda\) is the Nuclear Interaction Length. The interaction probability \(p_i=1-p_s\).
One can reproduce uniform distribution of interactions in the target setting very large value of \(\Lambda\).
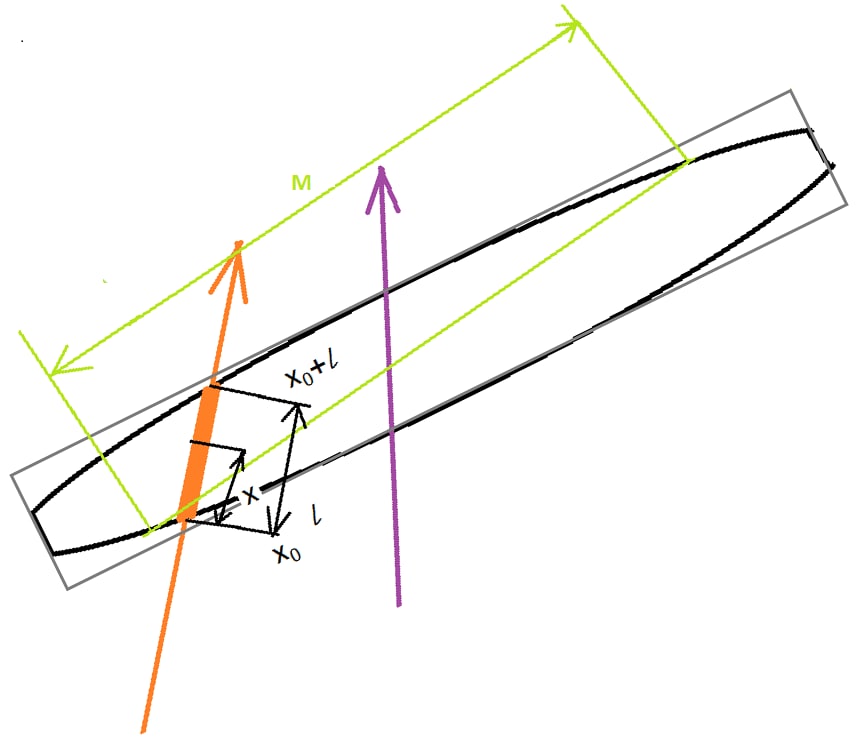
The path \(l\) of an ion passing without interaction through the target of an arbitrary convex shape along given trajectory depends on the position and orientation of the ion trajectory (scattering neglected). The longer is the \(l\) the greater is the interaction probability for ions at the same trajectory. One can introduce so called maximum path length \(M\) such that any ion in the simulation has the path inside the target less than this value. The Maximum path length is used for renormalization of the interaction probability for each trajectory:
Thus for the hypothetical trajectory with the maximum path length inside the target the interaction must happen (\(R_i=1\)). Renormalization of the interaction probability allows to minimize the number of the ions sampled in MC preserving correct spatial distribution of the interaction points.
In the picture below the target is black, the beam axis is magenta, the trajectory of an ion is orange, the maximum possible path of an ion in the target \(M\) is green. The path inside the target is thick orange, it has the length \(l\). \(X\) - is the interaction point. \(X_0\) and \(X_0+l\) - the points where the trajectory of the ion crosses the target boundary.
The ion transport in the target is controlled by the following interfaces.
- This value defines how steep is the exponential distribution of the interaction points inside the target along the trajectory:
interaction->SetNuclearInteractionLength(20.);
- The value which is greater than the path in the target for any possible ion:
interaction->SetMaxPathLength(0.051);
- Interaction should happen in following geometry volume:
interaction->SetInteractionVolumeName("tubeD2");
- To control coordinate resolution one need to control max step of transport:
interaction->SetMinStep(1e-5);
- But for thick target one need to remember about limit of max step count (specified in g4Config.C) in volume:
geant4->SetMaxNStep(30000);
In the ER simulations the \(R_i\) and \(X\) are sampled for each incident ion, which is either transported by G4, undergoing EM interactions like energy loss and multiple scattering, till the interaction point (defined along the simulated trajectory) or killed. The 4-momentum of the ion in the interaction point is used for calculation of the reaction products’ 4-momenta in the interaction point.
On the user request transport of an incident ion till the given energy (for resonance reactions) and till the point distributed according to user defined tabulated distribution can be easily implemented.
Elastic scattering¶
Постановка задачи упругого рассеяния¶
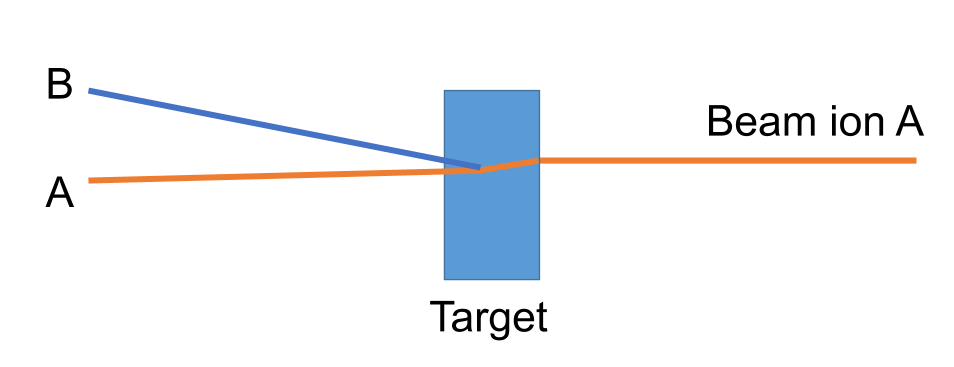
Ион А с энергией A E0 , импульсом A P0 (Px , Py , Pz ), начальными пространственными координатами A r0 (x0 , y0 , z0 ) налетает на покоящуюся мишень состоящую из атомов B. Ион A многократно рассеивается внутри объёма мишени, на некотором шаге выбивает ион B, и далее уже оба иона многократно рассеиваются пока не покинут объем мишени. В результате - новые характеристики A E, A P(Px , Py , Pz ), A r(x, y, z)- для иона А, и следующие для иона B: B E, B P(Px , Py , Pz ), B r(x, y, z).
Рассмотрим добавления упругого рассеяния в сессию симуляции на примере рассеяния иона 15N на мишени 11B. Создаем класс коллекции взаимодействий и класс взаимодействия:
ERDecayer* decayer = new ERDecayer();
ERElasticScattering* scattering = new ERElasticScattering("15Nto15N11B");
15Nto15N11B - Имя взаимодействия.
Входные данные¶
Пользователь должен знать:
Следующие характеристики ионов:
- A - атомная масса
- Z - число протонов
- Q - заряд
Для налетающего иона, например для 15 N, данные характеристике задаются так:
scattering->SetInputIon(7,15,3); // Z = 7, A = 15, Q = 3
А для иона мишени, например 11 B так:
scattering->SetTargetIon(5,11,5); // Z = 5, A = 11, Q = 5
Способ определения кинематических характеристик.
По умолчанию, используется изотропное распределение угла рассеяния ϴ.
Возможно задание кумулятивной функции распределения:
Задаём имя текстового файла с данными о кумулятивной функции:
scattering->SetThetaCDF("cos_tetta_cross.txt");
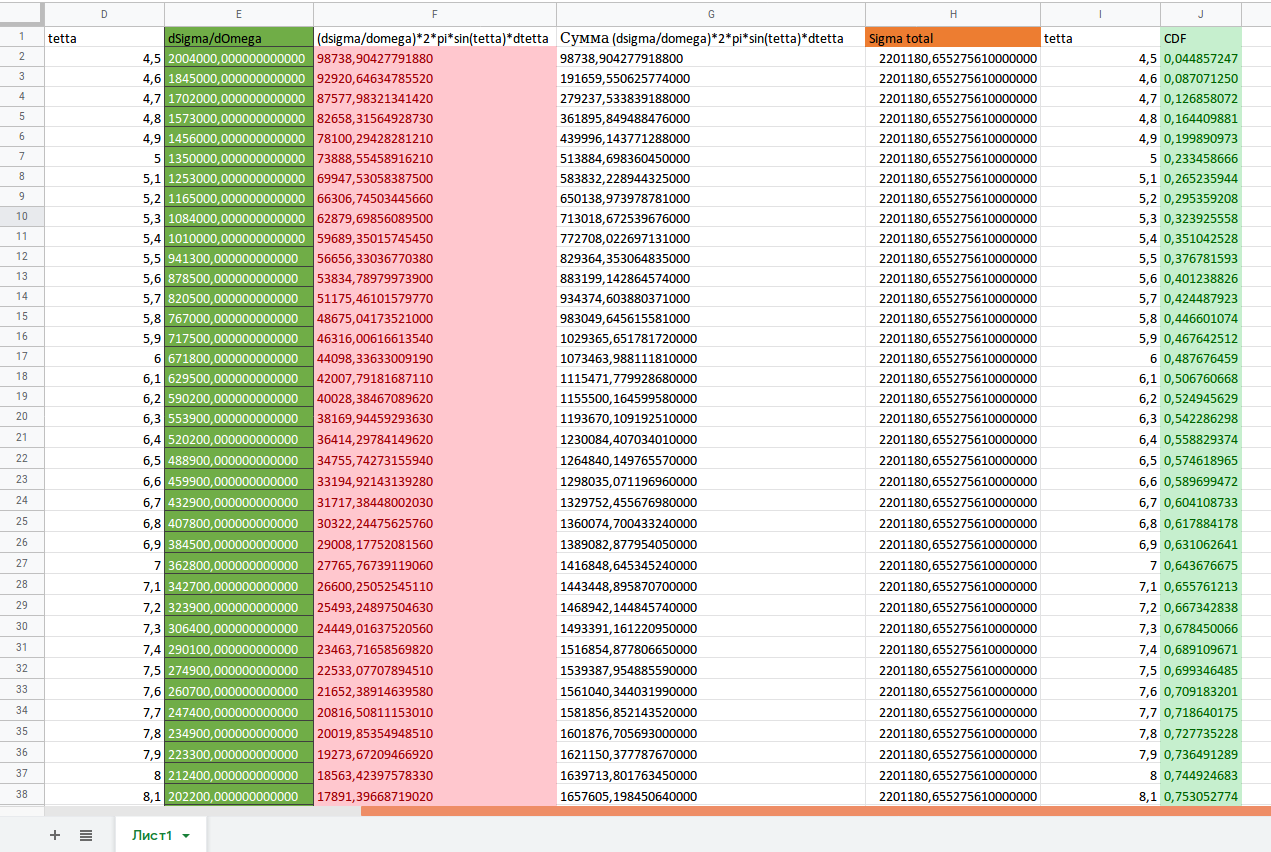
Структура текстового файла должна быть следующая:
4.5 0.0448573496944 4.6 0.087071447189 4.7 0.126858356665 4.8 0.164410246312 4.9 0.199891413123 5.0 0.233459173925 5.1 0.26523651571 5.2 0.295359837723 ... ... 179.3 0.99999999789 179.4 0.999999998493 179.5 0.999999998995 179.6 0.999999999397 179.7 0.999999999698 179.8 0.999999999899 179.9 1. 180.0 1.
Где первый столбец соответствует углам ϴ в системе центра масс, а второй — значениям кумулятивной функции для данных значений углов ϴ. Текстовый файл с данными о кумулятивной функции должен лежать в директории er/input .
Способ определения координаты взаимодействия.
Для изотропного розыгрыша координаты взаимодействия внутри объёма мишени. Задать переднюю координату мишени и заднюю относительно глобальной оси z:
scattering->SetUniformPos(-0.00035,0.00035);
Tip
Использовать в случае тонкой мишени.
Обычно мишень располагается в начале глобальной системы координат, данный рисунок иллюстрирует этот случай.
Для экспоненциального розыгрыша координаты взаимодействия, используйте метод:
SetExponentialPos(Double_t start, Double_t tau);
Tip
Использовать в случае толстой мишени.
Точность необходимую для определения положение координаты взаимодействия.
Для этого задаем шаг пророгации внутри объёма мишени:
scattering->SetStep(0.00001); //0.1 micron
Способ выбора диапазона розыгрыша углов ϴCM и φCM для выбираемой частицы.
По умолчанию ϴCM разыгрывается внутри диапазона от 00 до 1800 ,а φCM от 00 до 3600 . Если же стоит задача измерения эффективности (отношения сигнала к фону) отдельно стоящего детектора, а не целого экспериментального сетапа, стоит ограничить диапазон углов (соответствующий телесному углу, под которым виден детектор), чтобы не симулировать большое число событий, когда большее число продуктов реакции не попадают в детектор.
Выбрать диапазон розыгрыша ϴCM можно:
Явно:
scattering->SetThetaRange(18.4, 19.4, kPROJECTILE, relMod = kFALSE);
Косвенно. Через следующие величины:
Координату ϴLab центра диапазона розыгрыша.
Полуширину выбираемого диапазона 0.5*d ϴ в лабораторной системе координат:
scattering->SetLabThetaRange(thetaCenter, dTheta, kPROJECTILE, kTRUE, 0.);
Attention
Важно выбирать полуширину с запасом! Это значит, что нужно подбирать диапазон так, чтобы его дальнейшее увеличение не приводило к росту числа зарегистрированных событий.
В обоих случаях третьим параметром нужно передать симулируемую частицу, которая будет лететь в детектор. Этой частицей может быть:
- kPROJECTILE - налетающая частица.
- kTARGET - частица мишени.
Четвертый параметр, это мода для включения / выключения релятивизма.
Attention
По умолчанию установлен релятивизм! Что бы использовать калассичсекие формулы приведенные ниже, пользователь должет передать методу SetThetaRange четвертым параметром kFALSE.
Пятый параметр - среднее значение энергий пучка в GeV.
Attention
В релятивистском случае, нужно обязательно задать среднюю энергию пучка т.к она используется для расчета диапозона розыгрыша!
Для НЕ релятивистского случая углы пересчитываются по формулам, которые приведены ниже: ϴCM1 и ϴCM2 , где ϴCM1 и ϴCM2 крайние значения расчитываемого диапозона.
Когда M1 < M2
\[\begin{split}0 \leqslant \theta_1 \leqslant \pi\ ,\\\end{split}\]а когда M1 > M2
\[\begin{split}0 \leqslant \theta_1 \leqslant \theta_{1max} \leqslant \frac{\pi}{2}\ ,\\\end{split}\]в обоих случаях:
\[ \begin{align}\begin{aligned}\theta_{cm1} = \arccos\left [ -\frac{M_1}{M_2} + sin^2(\theta_1-d\theta) + cos(\theta_1-d\theta)\sqrt{1 - \frac{M_1^2}{M_2^2}sin^2(\theta_1-d\theta)} \right ]\ ,\\\theta_{cm2} = \arccos\left [ -\frac{M_1}{M_2} + sin^2(\theta_1+d\theta) + cos(\theta_1+d\theta)\sqrt{1 - \frac{M_1^2}{M_2^2}sin^2(\theta_1+d\theta)} \right ]\ .\end{aligned}\end{align} \]Когда M1 = M2
\[\begin{split}0 \leqslant \theta_1 \leqslant \frac{\pi}{2}\ ,\\\end{split}\]\[ \begin{align}\begin{aligned}\theta_{cm1} = 2(\theta_1-d\theta) ,\\\theta_{cm2} = 2(\theta_1+d\theta) .\end{aligned}\end{align} \]Для первоначально покоившихся частиц (во всех случаях):
\[ \begin{align}\begin{aligned}\theta_{cm1} = \pi - 2(\theta_2-d\theta) ,\\\theta_{cm2} = \pi - 2(\theta_2+d\theta) .\end{aligned}\end{align} \]M1 - масса налетающей частицы,
M2 - масса покоящейся частицы,
ϴ1 - угол рассеяния налетающей частицы (Лабе),
ϴ2 - угол вылета покоящейся частицы (Лабе).
d ϴ - полуширина выбираемого диапазона (Лабе).
Tip
Задавать диапазон розыгрыша косвенно: через координату ϴLab центра диапазона розыгрыша и полуширину выбираемого диапазона d ϴ - предпочтительнее! Эти параметры всегда известны пользователю, потому что все элементы геометрии позиционируется в Лабе!
Диапазон розыгрыша для φ выбирается явно:
scattering->SetPhiRange(-20., 20.);
Механизм работы класса¶
Добавляем упругое рассеяние в коллекцию распадов:
decayer->AddDecay(scattering);
Ниже опишем что будет происходить после этого.
Класс ElasticScattering содержит два основных метода: Intit(), Stepping().
Bool_t ElasticScattering::Init()¶
Данный метод вызывается в самом начале симуляции, на этапе инициализации.
Здесь проверяется:
if (!ERDecay::Init()) { return kFALSE; } fTargetIonPDG = TDatabasePDG::Instance()->GetParticle(fTargetIonName); if ( ! fTargetIonPDG ) { LOG(FATAL)<< "Target ion not found in pdg database!" << FairLogger::endl; return kFALSE; }Считается диапазон розыгрыша углов ϴCM - вызовом private процедуры:
ERElasticScattering::ThetaRangesLab2CM(Doubleр_t pM, Double_t tM)
где pM - масса налетающей частицы, а tM - частицы мишени.
Note
В случае явного определения диапазона розыгрыша ϴCM , метод описанный выше не вызывается!
Так же здесь формируется кумулятивная функция - вызовом private метода:
ERElasticScattering::ThetaCDFRead();
Bool_t ElasticScattering::Steping()¶
Вызывается на каждом шаге транспорта налетающего иона внутри объёма мишени.
Здесь разыгрываются углы вылета для ионов - налетающего и мишени, следующим образом:
// Generate random angles theta and phi
Double_t theta = ThetaGen();
Double_t phi = fRnd->Uniform(fPhi1*DegToRad(), fPhi2*DegToRad());
Метод:
ERElasticScattering::ThetaGen();
генерирует угол ϴCM из кумулятивной функции.
Затем ионы с новыми характеристиками кидаются в стек частиц для дальнейшего транспорта.
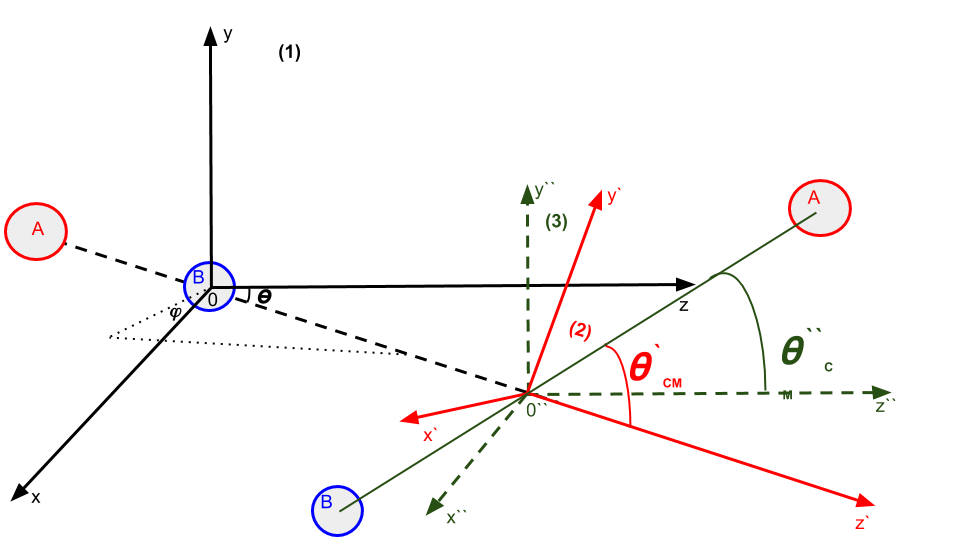
Связь лабораторной и центра масс систем¶
На рисунке выше ион А упруго рассеивается на ионе B. В имплементации метода ElasticScattering::Steping() углы ϴCM разыгрываются в системе координат (на рис., выше выделена красным) у которой ось z направлена вдоль импульса первичного иона. Необходимо повернуть систему координат (2) так что бы ее ось z совпала с-осью z из (3). С помощью методов TLorentzVector:
TLorentzVector::RotateZ(-phi);
TLorentzVector::RotateY(theta);
TLorentzVector::RotateZ(phi);
В стек частиц упруго рассеявшаяся ионы необходимо передать с характеристиками в лабораторной системе координат: Px, Py, Pz и E - энергия. Для перехода из системы центра масс в лабораторную используется Boost:
TLorentzVector::Boost(TVector3 &);
Подробнее об этом можно прочесть здесь: https://root.cern/doc/v616/classTLorentzVector.html
Полезные методы¶
Метод возвращающий число взаимодействии в мишени по всем событиям в run-е:
scattering->GetInteractNumInTarget();
Метод возвращающий среднее арифметическое ϴCM по всем событиям в run-е:
scattering->GetThetaCMMean();
Метод возвращающий массу налетающего иона:
scattering->GetProjectileIonMass();
Метод возвращающий массу иона мишени:
scattering->GetTargetIonMass();
Метод возвращающий величину диапазона кумулятивной функции (CDFMax-CDFMin):
scattering->GetdThetaCDF();
Пример использования класса¶
Класс ERElasticScattering использовался для моделирования упругого рассеяния15 N на 11 B.
Ниже представлен управляющий макрос для симуляции:
void sim(Int_t nEvents = 100, Int_t index = 0, TString outDir="output", Double_t angle = 20.)
{
gRandom->SetSeed(index);
//---------------------Files-----------------------------------------------
TString outFile;
outFile.Form("%s/sim_%d.root", outDir.Data(), index);
TString parFile;
parFile.Form("%s/par_%d.root", outDir.Data(), index);
// ------------------------------------------------------------------------
// ----- Timer --------------------------------------------------------
TStopwatch timer;
timer.Start();
// ----- Create simulation run ----------------------------------------
ERRunSim* run = new ERRunSim();
/** Select transport engine
* TGeant3
* TGeant4
**/
run->SetName("TGeant4"); // Transport engine
run->SetOutputFile(outFile.Data()); // Output file
// ------------------------------------------------------------------------
// ----- Runtime database ---------------------------------------------
FairRuntimeDb* rtdb = run->GetRuntimeDb();
// ------------------------------------------------------------------------
// ----- Create media -------------------------------------------------
run->SetMaterials("N15.media.geo"); // Materials
// ------------------------------------------------------------------------
//-------- Set MC event header --------------------------------------------
ERDecayMCEventHeader* header = new ERDecayMCEventHeader();
run->SetMCEventHeader(header);
//-------------------------------------------------------------------------
// ----- Create detectors ----------------------------------------------
FairModule* cave= new ERCave("CAVE");
cave->SetGeometryFileName("cave.geo");
run->AddModule(cave);
FairModule* collimator = new ERCollimator(); // "N15B11_collimator", "N15B11_collimator"
collimator->SetGeometryFileName("N15.collimator.root");
run->AddModule(collimator);
ERDetector* target = new ERTarget("N15B11_target", kTRUE, 1);
target->SetGeometryFileName("N15.target.root");
run->AddModule(target);
FairDetector* detector = new ERN15B11Detector("N15B11detector", kTRUE, 1);
detector->SetGeometryFileName("N15B11_detector.geo.root");
run->AddModule(detector);
//------ ER Decayer -------------------------------------------------
//Ion 15N
Int_t A = 15;
Int_t Z = 7;
Int_t Q = 3;
ERDecayer* decayer = new ERDecayer();
ERElasticScattering* scattering = new ERElasticScattering("15Nto15N11B");
scattering->SetInputIon(Z,A,Q);
scattering->SetTargetIon(5, 11, 5); // 11B
scattering->SetThetaCDF("cos_tetta_cross.txt");
scattering->SetUniformPos(-0.00035,0.00035);
scattering->SetStep(0.00001); //0.1 micron
scattering->SetDecayVolume("cave"); //targetB11
scattering->SetDetectorsSlot(angle, 4.*0.262822833);
scattering->SetPhiRange(-20., 20.);
decayer->AddDecay(scattering);
run->SetDecayer(decayer);
// ----- Create PrimaryGenerator --------------------------------------
FairPrimaryGenerator* primGen = new FairPrimaryGenerator();
ERIonMixGenerator* generator = new ERIonMixGenerator("15N", Z, A, Q, 1);
generator->SetKinERange(0.0427094, 0.0436017); // 0.0427094 : 0.0436017
Double32_t theta = 0.;
Double32_t sigmaTheta = 5e-3*TMath::RadToDeg();
generator->SetThetaSigma(theta, sigmaTheta); // theta = 0., sigma = 5 mrad
generator->SetPhiRange(0., 180.); // 0 : 180
Double32_t distanceToTarget = 50.; // work: 50 cm, test 0.5 micron: 0.00005+0.00035
generator->SetBoxXYZ(-0.5, -0.5, 0.5, 0.5, -distanceToTarget); // Xmin = -0.5, Ymin = -0.5, Xmax = 0.5, , Ymax = 0.5, Z
primGen->AddGenerator(generator);
run->SetGenerator(primGen);
// ------------------------------------------------------------------------
//-------Set visualisation flag to true------------------------------------
run->SetStoreTraj(kFALSE); // or kTRUE
//-------Set LOG verbosity -----------------------------------------------
FairLogger::GetLogger()->SetLogVerbosityLevel("LOW");
FairLogger::GetLogger()->SetLogScreenLevel("DEBUG");
//------- Initialize simulation run ---------------------------------------
run->Init();
Int_t nSteps = -15000;
//--- Runtime database ----------------------------------------------------
Bool_t kParameterMerged = kTRUE; /** @brief Returns curent theta in CM for Primary Ion. **/
FairParRootFileIo* parOut = new FairParRootFileIo(kParameterMerged);
parOut->open(parFile.Data());
rtdb->setOutput(parOut);
rtdb->saveOutput();
rtdb->print();
// ----- Run simulation ------------------------------------------------
run->Run(nEvents);
// ----- Finish -------------------------------------------------------
timer.Stop();
Double_t rtime = timer.RealTime();
Double_t ctime = timer.CpuTime();
cout<< endl << endl;
cout<< "Macro finished succesfully." << endl;
cout<< "Output file is sim.root" << endl;
cout<< "Parameter file is par.root" << endl;
cout<< "Real time " << rtime << " s, CPU time " << ctime
<< "s" << endl << endl;
}
Результаты моделирования¶
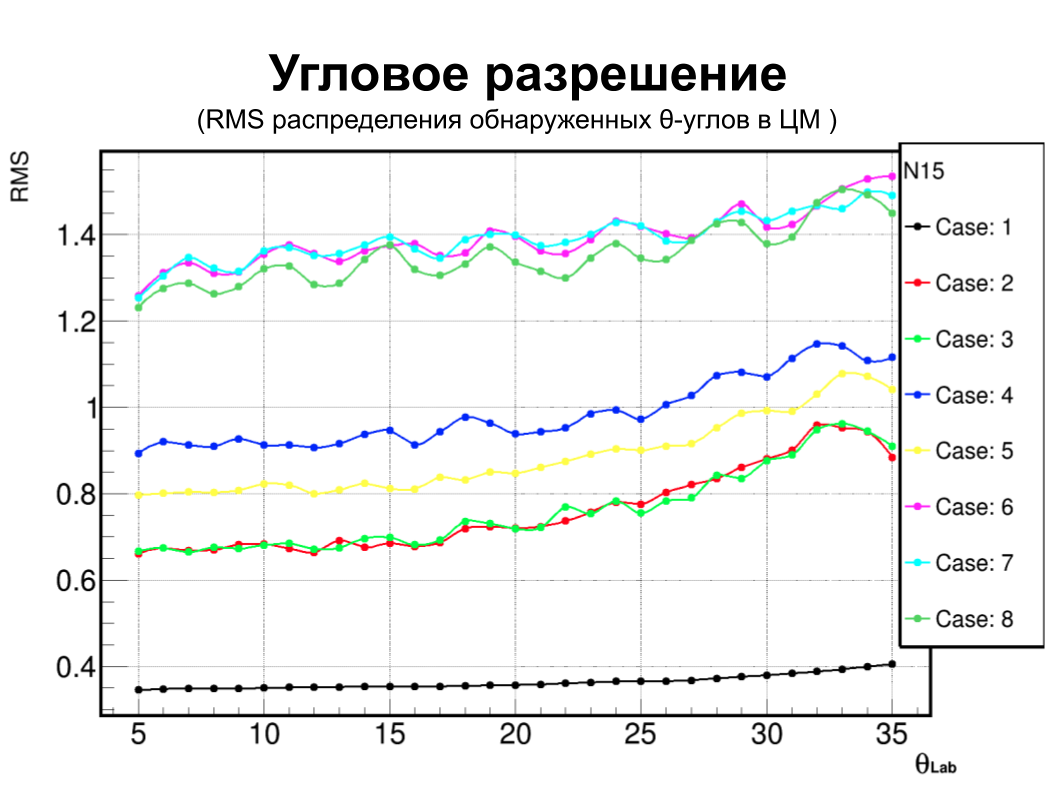
На данном рисунке мы отоброзили как некоторые физические факторы влияют на угловое разрешение.
- Мы начали с идеальной реакции с идеальным пучком, без мишени, без коллиматора, но с реалистичной щелью детектора и последовательно добавили следующие реалистичные свойства:
- 11B мишень толщиной 7 микрон
- Энергетическое размытие пучка иона 15N (42 : 43 МэВ)
- Размытие угла пучка иона 15N (sigma = 5 мрад)
- Размытие угла пучка иона 15N (0 : 2)
- X размытие пятна пучка на мишени (-0.5 : 0.5 см)
- Y размытие пятна пучка на мишени (-0.5 : 0.5 см)
- Коллиматор пучка (размер отверстия 1.5 см)
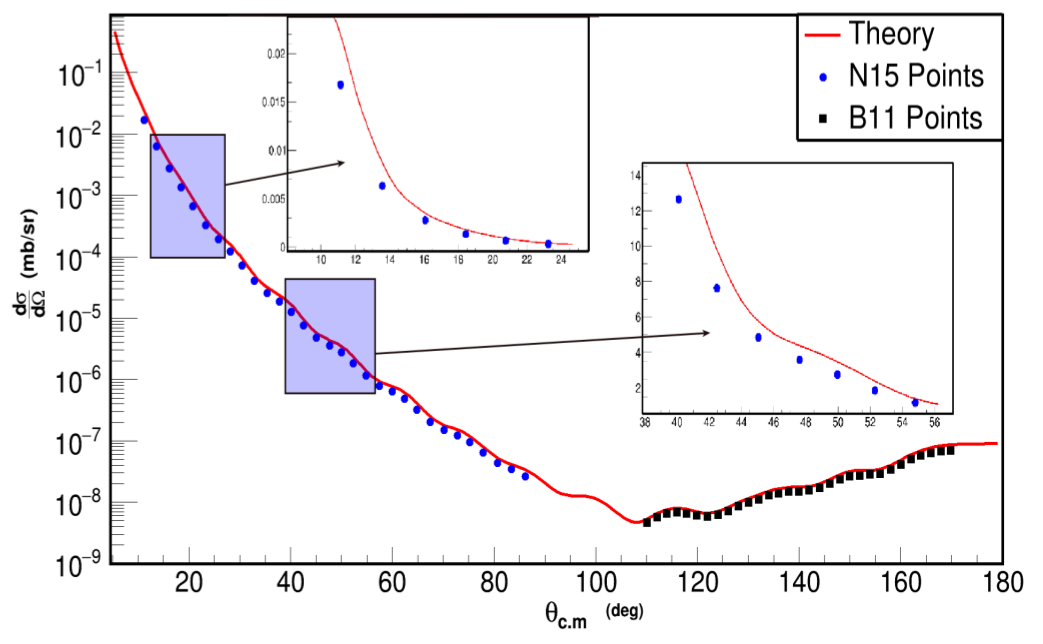
Измеренное дифференциальное сечение как функция угла рассеяния в ЦМ
На данном рисунке представлено сравнение входного дифференциального сечения и выходного (полученного по результатам симуляции). Здесь можно видеть два главных эффекта:
- Полученная зависимость становиться менее крутой в передних углах.
- Волновое поведение исходной кривой становится менее выраженным.
В результате работы было продемонстрировано, что восстановленное дифференциальное сечение немного отличается от входного Основной причиной этого различия является размер пятна пучка на мишени Влияние длины щели оказалось незначительно, следовательно, она может быть увеличено для лучшей эффективности обнаружения Разработанное программное обеспечение будет использоваться для планирования и анализа подобных экспериментов в будущем.
Interaction class¶
Реализация своего взаимодействия добавляется с помощью создания класса, унаследованного от ERDecay. Коды распадов расположены в дирeктории decays.
В новом классе необходимо написать реализации методов: Init, BeginEvent, FinishEvent, Stepping.
В методе Init необходимо проверить все ли ионы и частицы, которые учавствуют в распаде добавлены в объект распада и в Root библиотеку частиц - TDatabasePDG.
if (fInputIon) {
fInputIonPDG = TDatabasePDG::Instance()->GetParticle(fInputIonName);
if ( ! fInputIonPDG ) {
std::cerr << "ERTextDecay: Ion " << fInputIonName << " not found in database!"<< endl;
return kFALSE;
}
}
else{
std::cerr << "Input ion not defined"<< endl;
return kFALSE;
}
Также необходимо проверить все ли входные текстовые файлы и другие настройки распада указаны.
if (fFileName == "") {
cerr << "File for " << fName << " decay not defined!" << endl;
return kFALSE;
}
Метод BeginEvent вызывается в начале каждого события. Стандартно в этом методе необходимо реинициализировать часть переменных распада и разыграть вероятностные характеристики распада, в частности, позицию распада.
fDecayFinish = kFALSE;
if (fUniform){
fDecayPosZ = fRnd->Uniform(fUniformA, fUniformB);
}
if (fExponential){
fDecayPosZ = fExponentialStart + fRnd->Exp(fExponentialTau);
}
Метод Stepping вызывается на каждом шаге транспорта всех частиц. В нём закладывается условие распада и добавляются новые треки в стек треков. Типичная структура этого метода представлена далее.
Проверка того, что мы рассматриваем трекинг интересующего нас иона и установка малого шага трека для того чтобы максимально точно выбрать позицию распада:
if(!fDecayFinish && gMC->TrackPid() == fInputIonPDG->PdgCode()){
gMC->SetMaxStep(0.01);
gMC->TrackPosition(fDecayPos);
Провека что распад выполниться именно на этом шаге:
if (fDecayPos.Z() > fDecayPosZ){
gMC->TrackMomentum(fInputIonV);
//Add new ion
Int_t newTrackNb;
vector<TLorentzVector> decay = fDecays[gMC->CurrentEvent()];
Добавление новых частиц в стек для трнспорта:
gMC->GetStack()->PushTrack(1,gMC->GetStack()->GetCurrentTrackNumber(), fOutputIonPDG->PdgCode(),
outputIonV.Px(),outputIonV.Py(),outputIonV.Pz(),
outputIonV.E(), fDecayPos.X(), fDecayPos.Y(), fDecayPos.Z(),
gMC->TrackTime(), 0., 0., 0.,
kPDecay, newTrackNb, fOutputIonPDG->Mass(), 0);
Окончание распада. Остановка первичного иона. Возвращение максимального шага транспорта. Сохранение характеристик распада в объект MCEventHeader .
fDecayFinish = kTRUE;
gMC->StopTrack();
gMC->SetMaxStep(10000.);
SaveToEventHeader();
}
}
return kTRUE;
Decay definition in macro¶
Инициализация менеджера запуска.
void decay(Int_t nEvents = 10) {
//---------------------Files-----------------------------------------------
TString outFile= "sim.root";
TString parFile= "par.root";
// ------------------------------------------------------------------------
// ----- Timer --------------------------------------------------------
TStopwatch timer;
timer.Start();
// ------------------------------------------------------------------------
// ----- Create simulation run ----------------------------------------
ERRunSim* run = new ERRunSim();
run->SetName("TGeant4");
run->SetOutputFile(outFile.Data());
// ------------------------------------------------------------------------
// ----- Runtime database ---------------------------------------------
FairRuntimeDb* rtdb = run->GetRuntimeDb();
// ------------------------------------------------------------------------
// ----- Create media -------------------------------------------------
run->SetMaterials("media.geo"); // Materials
// ------------------------------------------------------------------------
Если необходимо сохранять параметры распада в выходной файл необходимо добавить MCEventHeader.
//-------- Set MC event header --------------------------------------------
ERDecayMCEventHeader* header = new ERDecayMCEventHeader();
run->SetMCEventHeader(header);
//-------------------------------------------------------------------------
Добавить необходимую геометрию в событие:
// ----- Create detectors ----------------------------------------------
FairModule* cave= new ERCave("CAVE");
cave->SetGeometryFileName("cave.geo");
run->AddModule(cave);
FairModule* target = new ERTarget("Target", kTRUE, 1);
target->SetGeometryFileName("Li10_target.geo.root");
run->AddModule(target);
// ------------------------------------------------------------------------
Добавить ERDecayer и добавить в него сконфигурированные распады:
//------ ER Deacayer -------------------------------------------------
ERDecayer* decayer = new ERDecayer();
ERDecay* targetDecay = new ERDecayLi9DetoLi10_Li9n_p();
decayer->AddDecay(targetDecay);
//-------------------------------------------------------------------------
Добавить генератор первичного иона.
// ----- Create PrimaryGenerator --------------------------------------
FairPrimaryGenerator* primGen = new FairPrimaryGenerator();
ERIonGenerator* ionGenerator = new ERIonGenerator("Li9",3,9,3,1);
Double32_t kin_energy = 0.025*9; //GeV
Double_t mass = ionGenerator->Ion()->GetMass();
Double32_t momentum = TMath::Sqrt(kin_energy*kin_energy + 2.*kin_energy*mass); //GeV
ionGenerator->SetPRange(momentum, momentum);
Double32_t theta1 = 0.; // polar angle distribution
Double32_t theta2 = 0.0001*TMath::RadToDeg();
ionGenerator->SetThetaRange(theta1, theta2);
ionGenerator->SetPhiRange(0, 360);
ionGenerator->SetBoxXYZ(-0.4,-0.4,0.4,0.4,-10);
primGen->AddGenerator(ionGenerator);
run->SetGenerator(primGen);
// ------------------------------------------------------------------------
Закончить инициализацию и запустить расчёт:
//-------------------------------------------------------------------------
// ----- Runtime database ---------------------------------------------
Bool_t kParameterMerged = kTRUE;
FairParRootFileIo* parOut = new FairParRootFileIo(kParameterMerged);
parOut->open(parFile.Data());
rtdb->setOutput(parOut);
rtdb->saveOutput();
rtdb->print();
//-------------------------------------------------------------------------
// ----- Run simulation ------------------------------------------------
run->Run(nEvents);
//-------------------------------------------------------------------------
// ----- Finish -------------------------------------------------------
timer.Stop();
Double_t rtime = timer.RealTime();
Double_t ctime = timer.CpuTime();
cout << endl << endl;
cout << "Macro finished succesfully." << endl;
cout << "Output file is sim.root" << endl;
cout << "Parameter file is par.root" << endl;
cout << "Real time " << rtime << " s, CPU time " << ctime
<< "s" << endl << endl;
//-------------------------------------------------------------------------
}
ERTextDecay - decay from text file¶
ERTextDecay - класс распада, в котором чтение результатов распада происходит из текстового файла следующей структуры:
10000 8.00 1.00 1.00 0.0000 10.0000 0.1653 0.3100 90.0000 -45.0000 1.0000 0.8000 1.0000
0.7206406E+01 -0.1754454E+02 0.5639178E+02 -0.1327796E+03 0.7652269E+00 -0.3139226E+02 0.7600432E+02 0.1677931E+02 -0.2499952E+02 0.5677531E+02 0.2169820E+00
0.9067860E+01 -0.2866158E+02 -0.3239947E+02 -0.9974271E+02 -0.1909192E+02 -0.4091810E+01 0.1072426E+03 0.4775351E+02 0.3649128E+02 -0.7499936E+01 0.1777150E+00
0.7098366E+01 -0.4391382E+02 -0.1458367E+02 0.1816315E+02 0.9634398E+02 0.1606081E+02 -0.2588241E+02 -0.5243016E+02 -0.1477139E+01 0.7719253E+01 0.2744438E+00
Первая строчка является шапкой файла и параметрами генерации. Данная информация не используется при реализации распада в ExpertRoot. Далее каждая строка в файле задает событие. Первое число - энергия возбуждения, также не используется в добавлении распада в транспорт. Далее записаны вектора импульсов выходов распада. Последняя колонка - угол реакции - тоже не используется.
Все импульсы указываются в системе центра масс распада. При чтении из файла импульсы переводятся в лабораторную СК с учётом импульса первичного иона в момент распада.
Все файлы распадов должны находится в папке input.
Для добавления данного распада в событие необходимо добавить в макрос:
//------ ER Deacayer -------------------------
ERDecayer* decayer = new ERDecayer();
ERTextDecay* decay = new ERTextDecay("10Heto8He2n");
decay->SetInputIon(2,10,2);
decay->SetOutputIon(2,8,2);
decay->AddOutputParticle(2212);
decay->AddOutputParticle(2212);
decay->SetDecayPosZ(2.);
decay->SetFileName("generator_10He_decay.dat");
decayer->AddDecay(decay);
run->SetDecayer(decayer);
При инициализации необходимо указать входной ион, выходной ион и набор выходных частиц через массовые числа или pdg. Далее необходимо указать позицию распада по Z и файл распада с импульсами выходных частиц.
Позицию распада также можно задать с помощью равномерного распределения. Это уместно для тонкой мишени.
SetUniformPos(Double_t a, Double_t b);
И с помошью экспоненциального распределения. Это уместно для толстой мишени.
SetExponentialPos(Double_t start, Double_t tau);